Рекурсивная формулировка отношения можетзавладетъ
Рисунок 2. 13. Рекурсивная формулировка отношения можетзавладетъ.
Данное предложение на самом деле определяет все множество возможных ходов указанного типа, так как оно применимо к любой ситуации, сопоставимой с состоянием, имеющим место перед входом. Поэтому такое предложение иногда называют схемой хода. Благодаря понятию переменной, имеющемуся в Прологе, такие схемы легко на нем запрограммировать.
Два других типа ходов: "подвинуть" и "залезть" - легко определить аналогичным способом.
Главный вопрос, на который должна ответить наша программа, это вопрос: "Может ли обезьяна, находясь в некотором начальном состоянии S, завладеть бананом?" Его можно сформулировать в виде предиката
можетзавладеть( S)
где аргумент S - состояние обезьяньего мира. Программа для можетзавладеть может основываться на двух наблюдениях:
(1) Для любого состояния S, в которой обезьяна уже имеет банан, предикат можетзавладеть должен, конечно, быть истинным; в этом случае никаких ходов не требуется. Вот соответствующий прологовский факт:
можетзавладеть( состояние( -, -, -, имеет) ).
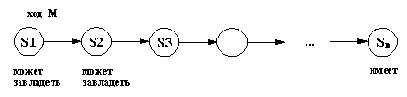
(2) В остальных случаях требуется один или более ходов. Обезьяна может завладеть бананом в любом состоянии S1, если для него существует ход из состояния Р1 в некоторое состояние S2, такое, что, попав в него, обезьяна уже сможет завладеть бананом (за нуль или более ходов). Этот принцип показан на Рисунок 2.13. Прологовская формула, соответствующая этому правилу, такова:
можетзавладеть( S1) :-
ход( S1, М, S2),
можетзавладеть( S2).
Теперь мы полностью завершили нашу программу, показанную на Рисунок 2.14.
Формулировка можетзавладеть рекурсивна и совершенно аналогична формулировке отношения предок из гл. 1 (ср. Рисунок 2.13 и 1.7). Этот принцип используется в Прологе повсеместно.
Мы создали нашу программу "непроцедурным" способом. Давайте теперь изучим ее процедурное поведение, рассмотрев следующий вопрос к программе:
?- можетзавладеть( состояние( удвери, наполу, уокна, неимеет) ).
Ответом пролог-системы будет "да". Процесс, выполняемый ею при этом, обрабатывает, в соответствии с процедурной семантикой Пролога, последовательность списков целей. Для этого требуется некоторый перебор ходов, для отыскания верного из нескольких альтернативных. В некоторых точках при таком переборе будет сделан неверный ход, ведущий в тупиковую ветвь процесса вычислений. На этом этапе автоматический возврат позволит исправить положение. На Рисунок 2.15 изображен процесс перебора.
line();% Разрешенные ходы
ход( состояние( середина, на ящике, середина, неимеет),
схватить,
% Схватить банан
состояние( середина, наящике, середина, имеет)).
ход( состояние( Р, наполу, Р, Н),
залезть,
% Залезть на ящик
состояние( Р, наящике, Р, Н) ).
ход( состояние( Р1, наполу, Р1, Н),
подвинуть( Р1, Р2),
% Подвинуть ящик с Р1 на Р2
состояние( Р2, наполу, Р2, Н) ).
ход( состояние( Р1, наполу, В, Н),
перейти( Р1, Р2),
% Перейти с Р1 на Р2
состояние( Р2, наполу, В, Н) ).
% можетзавладеть(Состояние):
обезьяна может завладеть
% бананом, находясь в состоянии Состояние
можетзавладеть( состояние( -, -, -, имеет) ).
% может 1: обезьяна уже его имеет
можетзавладеть( Состояние1) :-
% может 2: Сделать что-нибудь, чтобы завладеть им
ход( Состояние1, Ход, Состояние2),
% сделать что-нибудь
можетзавладеть( Состояние2).
% теперь может завладеть
line();
